|
1) Les
définitions

De nombreux essais ont étés réalisés en aviation
pendant la première et la 2ème guerre mondiale pour et optimiser les profils
afin d'améliorer les performances en fonction de paramètres précis, portance,
consommation de carburant, vitesse etc Les profils
NACA constituent la base de choix la plus importante.
On peut identifier un foil à partir d’une référence qui permet de le situer
en général.
Le premier chiffre caractérise la famille.
Le 2ème chiffre l'emplacement de la dépression minimum sur l'extrados
(4 signifie que la dépression minimum est à 120 mm du bord d'attaque pour un
foil ayant une corde de 300 mm)
Le 3ème chiffre (en petit caractère) la portance la plus favorable en ce qui
concerne la cavitation et le gradient de pression sur l'extrados.
Vient ensuite 3 chiffres qui donnent des information sur la forme
géométrique du profil (cambrure et épaisseur relative), puis plusieurs
chiffres donnant les dimensions du profil (corde et longueur)
L’élancement l du foil est égal au
rapport longueur foil / corde, dans le
cas présent 1400/ 300= 4,66
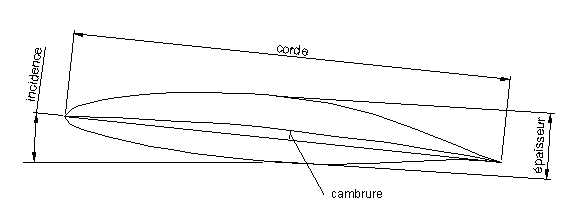
L’épaisseur
relative est égale à l’épaisseur divisée par la corde (e/C).
Elle s’exprime en % (de 6 à 8% pour un
foil mince et de 18 à 22% pour un foil épais).
La cambrure est aussi ramenée à la longueur de la corde. Elle peut varier de
2 à 6% pour les foils très cambrés.
L’incidence est l’angle que fait l’écoulement du fluide par rapport au plan
de la corde.
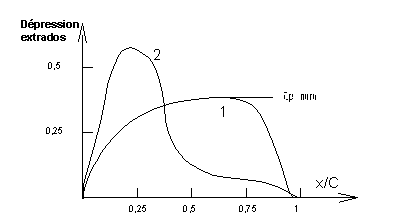
Les
2 courbes ci dessus permettent de comparer la
répartition de la dépression sur l’extrados le long de la corde pour 2 foils
d’épaisseur relative différente.
On remarque que dans le cas du foil mince (courbe 2) la dépression maximum
est plus importante et est décalée du coté du bord
d’attaque du foil.
Dans le cas d’un foil épais la dépression maximum est plus faible et est plus
à l’arrière du foil.
C'est
souvent la zone avant de l'extrados qui est en plus grande dépression.
Une plage d'incidence plus importante peut donc être obtenue sans cavitation
avec les foils épais.
Il est toutefois difficile de prédire à partir de la littérature existante
comment la dépression s'établit sur l'extrados en s'éloignant du bord
d'attaque.
Les courbes ci-dessus semblent
confirmer que les profils restant plus épais en se rapprochant du bord de
fuite permettent de maintenir plus longtemps le régime laminaire sur
l'extrados ce qui améliore la portance et le rapport portance/traînée aux
grandes incidences
2) Le nombre de
REYNOLDS
Le Nombre de Reynolds est un nombre sans dimension égal
à
Re = V c / n
V
La
vitesse de l’écoulement exprimée en m/s
c La corde du foil exprimée en m
n
La
viscosité cinématique de l'eau qui est par définition de 1 centistoke (10- 6 m²/s)
à titre d’exemple, à la vitesse de 10
m/s et avec un foil ayant une corde de
25 cm
(0,25 m) le nombre de Reynolds caractérisant
l’écoulement fluide a pour valeur :
Re = V c / n = 10 x 0,25 /10- 6 = 2,5 10 6
La traînée est sensiblement
affectée par un faible nombre de Reynolds.
L'écoulement, laminaire à basse vitesse devient turbulent lorsque la vitesse
et le nombre de Reynolds augmente. Lorsque l'écoulement est laminaire les
particules de fluide ont un écoulement régulier, par contre en écoulement
turbulent elles sont animées d'un mouvement tourbillonnaire.
Nota L'avance technologique du domaine aéronautique par rapport
aux techniques utilisées dans la navigation de plaisance est importante.
Le fait qu'une embarcation navigue à la limite entre l'air et l'eau complique
ce transfert technologique. Dans le domaine aéronautique les bancs d'essais
permettent de trouver les performances d'un profil donné lorsqu'il est
utilisé dans l'air et pour des nombres de REYNOLDS habituellement
relativement élevés.
Pour profiter de ces essais il convient d'extrapoler de l'air à l'eau en
tenant compte de la différence de viscosité cinématique et de densité entre
les 2 fluides.
Par
définition, à la température de 20°C, l'eau à une viscosité cinématique de 1
centistoke (ou 10-6 m²/s) alors que celle de l'air à la
même température est de 1,5 10-5 m²/s).
ll convient aussi de tenir compte de la
différence de densité (l'eau est 770 fois plus dense que l'air)
Pour un même nombre de REYNOLDS, le mouvement des particules étant comparable
qu'il s'agisse de l'eau ou l'air il est raisonnable de penser que les
performances d'un profil donné seront équivalentes avec les 2 fluides.
3) Les efforts
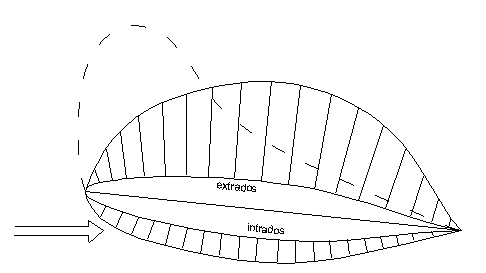
Contrairement
à ce que l’on pourrait penser l’effort de poussée fourni par le foil est plus
dû à la dépression sur l’extrados qu’à
la surpression sur l’intrados. On estime que, selon le type de profil,
l'intrados fournit seulement 25 à 30% de l'effort de poussée global.
La
courbe des dépressions sur l ‘extrados est très influencée par
l’incidence et l’épaisseur relative du foil.
La courbe en pointillée montre ce que pourrait être la dépression le long de
l’extrados pour un foil plus mince que celui représenté sur la figure et avec
la même incidence.
Pour une vitesse d'écoulement de l'ordre de 15 m/s (soit environ 30 noeuds) les valeurs de dépression maximum sur l'extrados
d'une voile sont environ 100 fois plus faibles que celles mesurées à la
même vitesse sur le profil ci-dessus avec de l'eau (0,001 bar contre 0,15
bar). Cette différence s'explique par la différence de viscosité et de
densité entre les 2 fluides et une différence entre les 2 écoulements (dans
l'air l'écoulement est turbulent alors qu'il est plutôt linéaire dans l'eau
au moins pour des incidences raisonnables)
Les
efforts des foils sont de 2 natures la
portance et la traînée
La
portance
FL = ½ r S V²
CLl avec CLl
= k CL¥
La traînée FD = ½ r S V² CD
avec :
r densité de l’eau soit 1000 kg/m3
V vitesse en m/s
CLl coefficient de portance tenant compte
des effets d’extrémité
S surface du
foil en m²
CD Coefficient de
traînée du foil
Exemple
à
10 m/s un foil ayant :
- Une surface S
de 0,5 m²
- Un élancement
l
de 4 entraînant un
coefficient de portance
CLl de 0,3
- Un coefficient de traînée CD
de
0,008
fournira :
un
effort de portance de FL = ½ 1000 x
0,5 x 10² x 0,3 = 7500 N soit 750 daN
et
aura une traînée de FD =
½ 1000 x 0,5 x 10² x 0,008 = 200 N soit 20 daN
ce qui représente dans le cas présent un excellent rendement.
Plaque plane
D'après Inge L.RYHMING (voir dynamique
des fluides de la presse polytechnique Romande de l'école de Lausanne édition
1984 p.165 à 171)
la force normale FN agissant
sur une surface plane de longueur L=4a et
de largeur égale à l'unité et en négligeant les effets d'extrémité est
égale à :
FN
= 4p a r v2
sina cosa a étant
l'incidence
Cet effort n’est pas ridicule si on le
compare à celui des profils élaborés ci-dessus.
(ski nautique et pourquoi pas ski de neige!)
4) La polaire du
foil
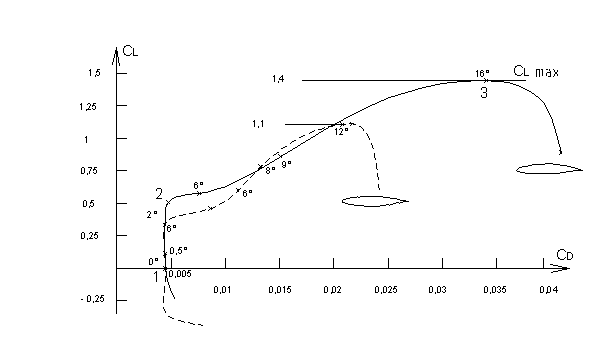
La polaire du foil est une courbe
importante qui quantifie les performances du foil, a savoir le rapport entre sa portance (lift) et sa
traînée(drag), lorsque son incidence varie.
La polaire est tracée pour un nombre de REYNOLDS donné car les performances
du foil varient sensiblement avec la vitesse de l'écoulement.
Au point 1 la portance est nulle indépendamment de la vitesse.
C’est au point 2 que le foil à les meilleures performances. CL/CD
maximum
Le rapport CL / CD traduit la finesse du foil
Au delà d’une certaine incidence (point 3) les performances
se dégradent brutalement, on dit que le foil ''décroche''.
Le foil symétrique est plus simple de construction mais n’a pas des
performances aussi bonnes que les foils cambrés (courbe en pointillée)
5) Les perturbations
51 Les effets d'extrémité du foil

La formule
de Von MISES met en évidence un coefficient de portance
tenant compte des effets d’extrémité et de l'élancement l
du foil.
Ce coefficient k =1/( 1 + 2/l ) diminue
avec l et
permet de mettre en évidence un coefficient de portance plus proche de la
réalité égal à
CL l = k CL ¥
soit CL l = CL ¥ /( 1 + 2/l )
La courbe ci-contre montre comment évolue la
portance en fonction de l’élancement l du
foil.(exemple un
foil ayant un élancement de 3 pert environ 40% par
rapport à son efficacité théorique)
Nota Lorsque
la vitesse augmente les foils de la 1ère génération sont de moins en
moins immergés et ont un rendement allant en se dégradant. De plus avec ces
foils l’air ambiant à tendance à s’infiltrer le long de l’extrados en
dépression ce qui augmente les risques de cavitation du foil
(il est rajouté des petits volets // à l'écoulement appelés ''fences'' qui limitent les entrées d’air)
.
Ils présentent l'avantage de s'asservir automatiquement en hauteur.
Les voiles comme les foils ont un meilleur rendement lorsque leur allongement
augmente.
|
Foil principal du type 1ère génération
(catamaran de Techniques avancées).
La partie verticale permet de résister aux efforts de dérives et donne de
la stabilité directionnelle.
On remarque que les ''fences" ne sont pas
nécessaires sur la face du foil en surpression (intrados)
|

|
|
Foil arrière 2ème génération du speed fun
Le
foil est monté à l'extrémité du safran. Il est parfois prévu des "fences" sur
le plan vertical.
Le bulbe améliore la rigidité mais provoque une traînée supplémentaire
|

|
52
La cavitation
Le s de cavitation est un paramètre
important dont la signification est développée dans le livre de Yves LECOFFRE .
Il est caractérisé par la formule
s =
(p amont - pV ) / ½ r V² avec
pamont Pression en amont du foil ( 1 bar = 105
pascal)
pV Tension de vapeur de l'eau
2500 Pascal à 20 °c
5000 Pascal à 30°c
r Densité de l'eau (1000 kg/m3)
soit à 30°C
s
= (105 - 5000 ) / ½
1000 V²
et s = 190 / V²
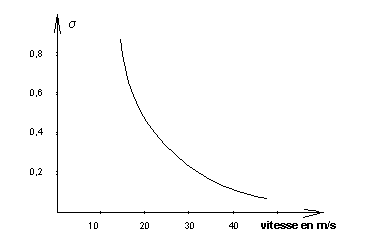
La formule
visualisée par la courbe ci-dessus caractérise la vitesse limite pouvant être
obtenue.
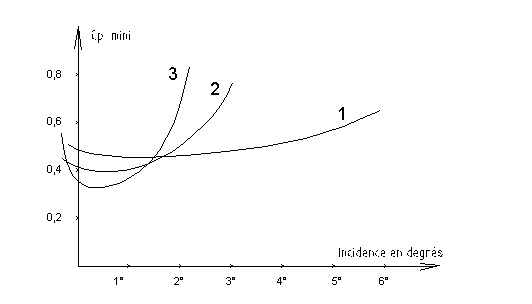
Il y a cavitation si Cpmin est plus
important que le s
de
cavitation
Courbes montrant l’évolution du Cp mini en fonction de l’incidence du foil.
Courbe 1
On dispose d’une plus grande plage d’incidence avant que le foil ne cavite avec les foils ayant une épaisseur relative
importante.
Courbe 3
Un foil mince est plus ‘’pointu’’. Il va certes avoir de meilleures
performances à faible incidence mais sur une plage d'incidence très réduite.
Il va ''décrocher'' plus vite et ne supporter qu’une petite variation
d’incidence.
Il
est préférable pour éviter la cavitation et ses conséquences (perte de
rendement et bruits) de prévoir des foils ayant une épaisseur relative
suffisante. Il a été constaté des niveaux sonores à l'intérieur des coques
extrêmement importants (supérieurs à 110 db),
lors de la dernière course transatlantique the Race. L'origine de ces
bruits peut s'expliquer par une cavitation des foils retransmettant à la
coque des vibrations haute fréquence. Le niveau sonore important et
extrêmement désagréable, presque métallique, d'une pompe hydraulique
qui cavite donne une idée de ce qu'on dû supporter
pendant plusieurs mois les équipages engagés dans cette course.
L’important si l’on souhaite
allez vite est donc de diminuer autant que faire se peut la pression
spécifique sur les foils en utilisant des foils de grande surface ceci afin
de diminuer le Cp min
Exemple:
avec un
s
de
cavitation de 0,2 bar, la vitesse limite est voisine de 30 m/s
|
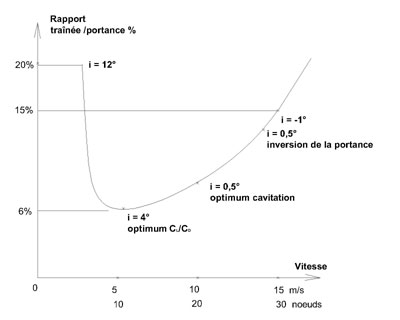
La courbe ci-contre donne une vision d'ensemble
du comportement d'un foil 2ème génération utilisé dans le contexte d'un
flotteur oscillant auto adaptatif
1) à basse vitesse le rendement du foil est affecté par un NB
de Reynolds peu élevé et le mauvais Cl/Cd à grande incidence. La
traînée augmente notablement.
Un effort de propulsion assez important est donc nécessaire au démarrage.
2) lorsque la vitesse augmente l'incidence diminue et le rendement
s'améliore considérablement . Lorsque l' incidence devient négative la trainée augmente à
nouveau et la poussée s'inverse , ce qui explique pourquoi le
flotteur oscillant auto adaptatif est naturellement stable.
|
|
BIBLIOGRAPHIE
Mécanique
appliquée de R. OUZIAUX et J.
PERRIER éditeur DUNOD Tome 1 Pages
257 à 295
Dynamique des Fluides de INGE L.
RYHMING éditeur presses
polytechniques Romandes. Pages
164 à 170
Théory
of wing sections by IRA H. ABBOTT et E. VON DOENHOFF
r
Recueil de profils NACA 16-012, 664-021, 66-009,
mean line serie
66, 662-215, 663-218, 663-418, 664-221
Mécanique expérimentale des
fluides Tome 2 de R.
COMOLET éditeur
MASSON Pages 265 à 279
Engineering
fluid mechanics de ROBERSON and
CROWE 5ème édition Pages 502 et
518 à
525
Computational Fluid dynamics de John F.
WENDT
5ème édition Page 71
Le nouveau cours de navigation des Glénans édition
du SEUIL 1995
5 ème édition page 209 polaire
d'une voile
Dynamique
du navire de P.
DEVAUCHELLE
éditeur
MASSON Pages 92 et
93
Fundamental
of fluid mechanics de
Bruce R.Munson Pages 618
et 619
Introduction to fluid mechanics
de Robert W. FOX 4 ème édition. Pages 448 à 455
Extrait
de livres traitants de la
cavitation Essais
expérimentaux avec profil NACA 16-012
Retour
en haut de la page
|





